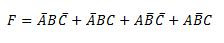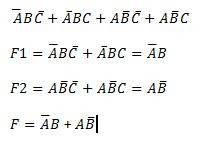Format Penyandian Sinyal Digital - Format Multilevel Binary

Format Pengodean ini diarahkan untuk mengatasi ketidak efisienan kode NRZ. kode ini menggunakan lebih dari 2 level sinyal (contohnya anda dapat lihat pada gambar dibawah).

Bipolar AMI, yaitu suatu kode dimana biner '0' diwakili dengan tidak adanya garis sinyal dan biner '1' diwakili oleh suatu pulsa positif atau negatif. sedangkan pseudoternari adalah suatu kode dimana biner '1' diwakili oleh ketiadaan garis sinyal dan biner '0' oleh pergantian pulsa positif dan negatif.

Keunggulan biner multilevel terhadapNRZ, yaitu :

1. Kemampuan sinkronisasi yang baik
2. tidak menangkap komponen dc dan pemakaian bandwidth yang lebih kecil
3. dapat menampung bit informasi yang lebih banyak.

Kekurangan dibanding NRZ, yaitu :

1. diperlukan pesawat penerima yang mampu membedakan 3 level (+A, -A, 0) sehingga membutuhkan lebih dari 3 db kekuatan sinyal dibanding NRZ untuk probabilitas kesalahan bit yang sama

Format Penyandian Sinyal Digital - Format Non Return to Zero

Format yang paling mudah dalam mentransmisikan sinyal digital adalah dengan menggunakan dua tingkat voltaseyang berlainan untuk dua digit biner .Kode-kode yang mengikuti cara ini dibagikan berdasarkan sifat-sifatnya. Tingkat voltase tetap konstan sepanjang interval bit yang ditransmisikan, yang dalam hal ini terdapat transisi (tidak kembali ke level voltase nol).

ngemeng-ngemeng.... ni format terbagi atas 2 macam, baca baik-baik ya...

1. Non-Return-to-Zero-Level (NRZ-L), yaitu suatu kode dimana tegangan negatif dipakai untuk mewakili suatu biner dan tegangan positif dipakai untuk mewakili biner lainnya.
2. Non-Return-to-Zero-Inverted, yaitu suatu kode dimana suatu transisi ( dari yang tinggi ke rendah atau dari yang rendah ke tinggi) pada awal suatu bit time akan dikenal sebagai biner '1' untuk bit time tersebut. Bila tidak ada transisi berarti biner '0'. Dengan demikian NRZI merupakan salah satu contoh dari differensial encoding.

woi... bro- bro dan siter-sister..... :)
nih keuntungan dari penyandian diferensial, antara lain : lebih kebal noise, tidak dipengaruhi level tegangan.
sedangkan kelemahan dari NRZ-L maupun NRZI yaitu: keterbatasan dalam komponen dc dan kemampuan sinkronisasi yang buruk.

contoh gambarnya bisa anda lihat dibawah ini :

semoga bermanfaat

PETA KARNAUGH EMPAT MASUKAN

Peta karnaugh untuk 4 masukan sebenarnya tidaklah jauh beda dengan Peta-K dengan 3 masukan. cukup dengan menambahkan 1 masukan pada sisi yang hanya memiliki 1 masukan. belum mengerti? ..... gini..... untuk baris kolom kita isikan masukan A dan B dan untuk barisnya untuk masukan C dan D . Peta Karnaugh dengan 4(empat) masukan jumlah selnya yaitu 2^4=16 sel. agar lebih mengerti disini saya akan meberikan sebuah contoh soal untuk Peta K denga 4 masukan:

wuihhhh..... panjang .... hehe
mari kita selesaikan, pertama kita perlu membuat peta Karnaughnya, seperti pada gambar dibawah ini:

tujuan dari peta diatas adalah agar mempermudah kita dalam mencocokkan soal dengan letak logikanya. kemudian kita isi sel yang cocok dengan soal diatas dengan nilai logika 1 dan yang bukan kita isi dengan nilai logika 0 sperti nampak pada gambar ke 2 dibawah:

setelah kita mengisi logika 1 sesuai dengan soal, maka kemudian kita kelompokkan sel yang bernilai logika 1 seperti pada gambar dibawah ini :

PETA KARNAUGH

Peta Karnaugh, apa sih peta Karnaugh itu? mmmm... apa ya... hehe....
sebelumnya tentu kita sudah mengenal Aljabar Boole. Aljabar boole dapat digunakan untuk menyederhanakan perancangan untaian logika. tetapi, cara ini mengandung operasi matematis yang cukup panjang. maka di carilah cara yang lain agar penyederhanaan untaian logika lebih mudah. Peta Karnaugh, adalah jalan keluarnya. Peta karnaugh (peta-K) atau diagram berdasarkan teknik pengenalan pola.

PETA KARNAUGH 2 MASUKAN
Peta Karnaugh berisi semua kemungkinan kombinasi dari sistem logika kombinasi ini dirangkai dalam bentuk tabel. adapun Peta Karnaugh yang paling sederhana adalah terdiri dari dua buah masukan atau peubah, yaitu A dan B seperti pada gambar (A). Kolom menyajikan masukan A, dengan kolom disebelah kiri menyajikan A=0 dan kolom disebelah kanan menyajikan A=1. masukan B akan dituliskan pada baris dengan baris pertama menunjukan B=0 dan baris kedua menunjukan B=1 . sehingga semua kemungkinan dari peubah dapat kita lihat dalam tabel , yaitu 4 buah masukan. jika kita mengungkapkannya dalam bentuk ungkapan Boole, maka ungkapan tersebut dituliskan sesuai dengan sel yang sesuai dengan masukannya.

sebagai contoh F=A.-B +A.B (A AND NOT B OR A AND B)


Peta Karnaugh contoh diatas dapat anda lihat pada gambar (B). dimana FI I (A=1,B=0) dan F2(A=1,B=1). kolom yang merupakan pertemuan kedua peubah maka kita beri angka "1" dan yang lainnya kita isi dengan angka "0". setelah itu, angka 1 yang berdekatan kemudian kita kelompokkan seperti tampak pada gambar (C). dalam kelompok tersebut kita melihat dimana A tidak akan berubah, tetap bernilai logika "1". tetapi, B dapat bernilai "1" atau "0" tanpa mempengaruhi keluarannya. sehingga ungkapan diatas dapat kita sederhanakan menjadi F=A . jika kita ungkapkan dalam bentuk ungkapan Boole maka :

F=A.-B +A.B
(#A+A= A)
(#-B+B=0)
F=A

PETA KARNAUGH 3 MASUKAN
untuk 3 buah masukan A,B, dan C, maka akan terdapat 2^3=8 buah kombinasi yang harus dituliskan kedalam peta-K . anda dapat melihatnya pada gambar (A). kombinasi A dan B tidak boleh dituliskan secara bebas pada kolom yang tersedia. kombinasi dari A dan B harus disusun dengan sedemikian rupa agar terjadi perubahan masukan dari satu sel ke sel berikutnya. hal ini juga berlaku pada ujungnya. sehingga, perbedaan dari ujung kanan dan ujung kiridari A adalah 1 dan 0, sementara pada B tetap pada 0. hal sama juga harus dilakukan pada ujung yang lain yaitu atas dan bawah.

(A) (B) (C)

Dimisalkan suatu ungkapan Boole :

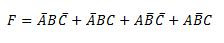
Peta-K dari ungkapan diatas tersaji pada gambar (B) diatas dengan logika 1 ditempatkan pada sel-sel sesuai dengan ungkapan berikut:
NotA.BNotC pada A=0, B=1, C=0
NotA.B.C pada A=0, B=1, C=1
A.NotB.C Pada A=1, B=0, C=1

kemudian sel-sel yang lain dapat di isi dengan logika 0. pada gambar diatas, anda dapat melihat dimana terdapat 2 kelompom 1 yang berdekatan. kelompok sebelah kiri menunjukan A=0 dan B=1 yaitu NotA.B. kelompok sebelah kanan menunjukkan A=1, B=0 yaitu A.NotB. nilai C tidak berpengaruh sehingga ungkapan diatas dapat disederhanakan menjadi NotA.B atau ANotB. ungkapannya sebagai berikut :

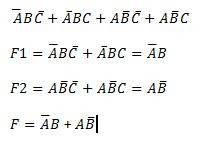
Semoga bermanfaat :)

Pengenalan Bahasa Pemrograman C++

Bahasa Pemrograman C++ adalah pengembangan dari bahasa pemrograman C sebagai pendahulunya. Bahasa Pemrograman C++ telah mendukung Pemrograman berorientasi objek seperti halnya bahasa pemrograman Java. Semua library yang ada pada bahasa C telah tercakup pada bahasa C++. Keterkaitan antara bahasa C dan C++ dapat anda lihat ada gambar dibawah ini .

Bahasa pemrograman C++ termasuk dalam bahasa pemrograman level tengah (middle level) yang berarti merpakan campuran elemen bahasa pemrograman tingkat tinggi (highest level) dan bahasa pemrograman tingkat rendah (lowest level) .

Level bahasa pemrograman ditentukan dengan dekatnya pengaksesan sistem komputer dengan bahasa pemrograman yang digunakan. misalnya bahasa pemrograman level rendah seperti assembler cara kerjanya sangat dekat dengan sistem komputer yang pada dasarnya hanya dapat mengeksekusi byte yang berisi angka 1 dan 0. begitu pula dengan pengecekan program saat runtime , semakin rendah level bahasa pemrograman, maka pengecekan error pada saat program dijalankan akan semakin terbatas, sehingga tak jarang tiba-tiba program menjadi hang saja. akan tetapi, bukan berarti semakin tinggi level bahasa pemrograman, maka bahasa pemrograman itu akan lebih tangguh, karena lebih kompleks tidak selalu lebih tangguh.

Bahasa Pemrograman C++ merupakan bahsa pemrograman yang bersifat case sensitive yang artinya penulisan dengan menggunkan huruf besar dan hruf kecil diartikan berbeda oleh compiler, misalnyapenulisan "printf" mempunyai arti yang berbeda dengan "Printf". sebagai gambaran berikut adalah contoh bahasa pemrograman C++ dengan algoritma membuat secangkir susu panas.

PERULANGAN REKURSIF DAN PERULANGAN ITERATIF

PERULANGAN REKURSIF DAN PERULANGAN ITERATIF

Rekursif adalah suatu proses yang bisa memanggil dirinya sendiri.
Perulangan Rekursif merupakan salah satu metode didalam pemrograman yang mana dalam sebuah fungsi terdapat instruksi yang memanggil fungsi itu sendiri, atau lebih sering disebut memanggil dirinya sendiri.
Perulangan iteratif merupakan perulangan yang melakukan proses perulangan terhadap sekelompok instruksi. perulangan dilakukan dalam batasan syarat tertentu. ketika syarat tersebut tidak terpenuhi lagi maka perulangan akan terhenti.

Persamaan:

• Iteratif dan rekursif merupakan metode atau teknik didalam perulangan (looping)
• Sama-sama memiliki bagian yang berfungsi sebagai batas dalam sebuah perulangan

Perbedaan:

• Iteratif dalam melakukan perulangan membutuhkan suatu instruksi program seperti for, repeat until dan while do, sedangkan rekursi tidak memakai instruksi program seperti itu. cukup dengan fungsi tersebut

Contoh penggunaan proses rekursif

• Masalah : Memotong roti tawar tipis-tipis sampai habis

• Algoritma :

1. Jika roti sudah habis atau potongannya sudah paling tipis maka pemotongan roti selesai
2. jika roti masih bisa dipotong, potong tipis dari tepi roti tersebut
3. lakukan prosedur 1 dan 2 untuk sisa potongannya

CONTOH FUNGSI REKURSIF
1. fungsi pangkat

• Menghitung 10 pangkat n dengan menggunakan konsep rekursif
• Secara notasi pemrograman dapat dituliskan sebagai berikut :

2. Faktorial

• 0! =1
• N! = N X (N-1)! untuk N>0
• Secara notasi pemrograman dapat dituliskan sebagai berikut :

FAKT(0) = 1 ...........................................(1)
FAKT(n) = N*FAKT(N-1).....................(2)

Contoh:
FAKT(5)= 5*FAKT(4)
FAKT(4)= 4*FAKT(3)
FAKT(3)= 3*FAKT(2)
FAKT(2)= 2*FAKT(1)
FAKT(1)= 1*FAKT(0)
nilai awal;

misalnya :
Hitung 5! dapat dihitung dengan cara rekursif sebagai berikut :
5! = 5*4 !
secara rekursif nilai dari 4! dapat dihitung kembali dengan cara : 4*3 !
sehingga 5! menjadi 5!= 5*4*3 !
secara rekursif nilai dari 3! dapat dihitung kembali dengan cara : 3*2 !
sehingga 5! menjadi 5!= 5*4*3*2 !
secara rekursif nilai dari 2! dapat dihitung kembali dengan cara : 2*1
sehingga 5! menjadi 5!= 5*4*3*2*1


3. Deret Fibonacci

• Deret fibonacci : 0, 1, 1, 2, 3, 5, 8, 13,...
• Secara notasi pemrograman dapat dituliskan sebagai berikut :

1. FIBO(1) = 0 dan FIBO (2) = 1 .....................................(1)
2. FIBO(N) = FIBO (N-1) + FIBO (N-2).........................(2)

contoh :
Fibo(5) = FIBO (4) + FIBO (3)
Fibo(4) = FIBO (3) + FIBO (2)
Fibo(3) = FIBO (2) + FIBO (1) -----> nilai awal

4. Konsep Menara Hanoi

• tujuan permainan ini adalah memindahkan n buah balok dari tonggak asal A melalui tonggak bantu B menuju tonggak C. dengan aturan balok yang lebih kecil tidak boleh berada di bawah balok yang lebih besar

bayangkan keadaan berikut :
ada 3 tiang (a, b, c) tempat balok dengan ukuran yang bervariasi dapat ditumpuk. pada mulanya semua balok ada di "A". Tugasnya adalah meindahkan semua balok ke "C" degan aturan sebagai berikut :

• Pada satu saat hanya boleh memindah 1 balok
• setiap perpindahan berupa pengambilan balok teratas dari satu tiang dan memasukkannya ketiang lain, diatas balok lain yang mungkin sudah ada pada tiang tersebut.
  
• tidak boleh meletakkan balok diatas balok lain yang lebih kecil
• pada setiap akhir pemindahan semua balok harus berada di tiang.

Dalam notasi algoritma dapat dituliskan sebagai berikut :

• jika n= 1, maka langsung pindahkan saja balok dari tiang A ke tiang C dan selesai
• pindahkan n-1 balok yang paling atas dari tiang A ke Tiang B
• pindahkan balok ke n (balok terakhir) dari tiang A ke tiang C
• pindahkan n-1 balok dari tiang B ke tiang C
  

Program sederhana untuk Mencari Nilai tahanan

berikut ini adalah program sederhana yang telah saya buat mengenai nilai tahanan resistor beserta toleransinya

untuk mendownload programnya silahkan klik link dibawah ini:
http://www.ziddu.com/download/14155998/nilaitahananresistor.exe.html

semoga bermanfaat

bentuk "program jadi" tugas logika dan algoritma

silahkan download bentuk program tugas logika dan algoritma , free!!!

tugas 1 konversi suhu
http://www.ziddu.com/download/14101415/Konversisuhu.exe.html


tugas 2 konversi jam ke menit dengan input jam dan menit
http://www.ziddu.com/download/14101522/KONVERSIMENIT.exe.html

tugas 3 masih dalam proses pembuatan

andy scevorz semoga bermanfaat........

Membuat Program sederhana dengan Visual BAsic 6.0

MENGHITUNG JUMLAH DERET ARITMATIKA DENGAN SUKU AWAL, BANYAK SUKU DAN BEDA DIKETAHUI

membuat program dengan visual basic bagi para pemula mungkin agak susah... seperti saya haha... tetap tak ada yang tak mungkin jika kita MAU. disini saya akan membagikan sedikit ilmu yang saya dapatkan tentang cara membuat program "menghitung jumlah deret aritmatika dengan suku awal, banyak suku dan beda diketahui"

1. Buka program Microsoft Visual Basic 6.0
2. klik file lalu pilih menu new Project dan pilih New standard .exe
3.lalu akan muncul Lembar kerja Project1-form1(form)
4. pada kotak tabel form1 kita buat :

• Buat 3 kotak label : label1, label2, label3
• Buat 4 kotak textbox : text1, text2, text3, dan text4
  
• Buat Tombol command : command1
• atur sedemikian rupa sesuai yang anda inginkan .... kalau punya saya sih seperti ini :

OK?......mungkin contoh tampilan tata letaknya seperti diatas . lanjut....

5. setelah tampilannya kita atur , sekarang kita atur nama dari masing masing label, text dan command1, pada tabel properties :

• label1 (name=label1 , backstyle=0-transparent, caption=suku awal)
• label2 (name=label2 , backstyle=0-transparent, caption= banyak suku)
• label3 (name=label3 , backstyle=0-transparent, caption = beda)
• text1 (name=text1 , alaignment=2-center, text = none)
• text2 (name=text2, alaignment=2-center, text = none)
• text3 (name=text3, alaignment=2-center, text = none)
• text4 ((name=text4, alaignment=2-center, text = none)
• command1 (name= command1, caption = jumlah)
• form1 (name= menghitung jumlah deret)
  

6. sekarang kita buat bahasa pemrogramannya, ketikkan text dibawah ini pada kotak view code. Kurang lebih seperti ini :

• Private Sub command1_click()
  hasil1 = Val(Text2) - 1
  hasil2 = hasil1 * Val(Text3)
  hasil3 = hasil2 + Val(Text1)
  hasil4 = Text1 + hasil3
  hasil5 = hasil4 * Text2 / 2
  jumlah = hasil5
  Text4 = jumlah
  End Sub

tampilannya akan seperti ini :

oh ya..... "name" disini sangat berpengaruh pada pembuatan bahasa program jika kita mengubah nama pada "name" maka pada program kita harus mengubahnya juga agar dapat dikenali. selain itu untuk warna anda dapat memilih sesuai warna yang anda inginkan dengan cara : clik objek yang warnanya ingin di ubah lalu klik backcolor lalu pilih warna.....

7. setelah itu save project
8. klik file lalu pilih make menghitung deret aritmatika.exe
9. selesai

untuk program yang udah jadi bisa anda download di :
http://www.ziddu.com/download/14093851/menghitungderetaritmatika.exe.html

ok... semoga bermanfaat :)

TOLERANSI PADA SEBUAH RESISTOR

      Pada umumnya pada badan resistor terudapat cincin warna ke empat, yangl ditempatkan pada ujung yang berlaawanan dengan ketiga cincin lainnya. cincin warna ini mengindikasikan toleransi atau tingkat kepresisian sebuah resistor. Cincin ini memberikan informasi kepada kita bahwa seberapa jauh nilai tahanan aktual resistor akan menyimpang dari nilai tahanan nominal yang dinyatakan oleh kode warna resistor.

      Misalnya seperti pada gambar disamping, seperti yang kita ketahui , kuning`4` , ungu`7` dan merah`2`. maka nilai yang kita dapatkan adalah 4700 ohm. lalu warna emasnya? ok..... cincin yang berwarna emas tersebut kita menyebutnya dengan toleransi seperti yang telah saya jelaskan diatas. lalu bagaimana cara menghitungnya?

setelah kita mendapatkan nilai resistor 4700 ohm maka kita perlu mengetahui berapa nilai toleransi dari cincin berwarna emas tersebut. cincin berwarna emas tersebut memiliki nilai toleransi (kurang lebih)5%. maka:

4700 ohm x 5/100 = 235 ohm
Dengan demikian nilai tahanan aktual resistor dapat berubah-ubah antara :

• 4700 - 235 = 4465 Ohm   

hingga

• 4700 + 235 = 4935 Ohm 

andy scevorz

DIAGRAM ALUR (FLOW CHART)

Flowchart adalah suatu diagram yang menggambarkan susunan logika suatu program atau dengan kata lain flowchart ialah diagram yang menggunakan simbol dan garis untuk menggambarkan urutan proses suatu logaritma, dimana simbol-simbol tersebut dihubungkan dengan garis berpanah. berikut ini simbol-simbol Flowchart dan penjelasannya :

Keterangan :
1. Proses/Processing satu atau beberapa himpunan penugasan yang akan dilaksanakan secara berurutan
2. Input/output data yang akan dibaca dimasukkan kedalam memory komputer dari suatu alat input
3. Terminal berfungsi sebagai awal (berisi"START") dan sebagai akhir (berisi "END") dari suatu proses alur
4. Decision (kotak keputusan) berfungsi untuk memutuskan arah / percabangan yang diambil sesuai               dengan kondisi yang dipenuhi, yaitu benar / salah.
5. Subroutine digunakan untuk menjalankan proses suatu bagian (sub program) atau prosedur
6. Preparation digunakan untuk pemberian harga awal
7. Connector / Penghubung digunakan untuk menghubungkan diagram alur yang terputus dimana                      bagian tersebut masih berada pada halaman yang sama.
8 On page connector untuk menghubungkan sambungan dari bagian flowchart yang terputus dimana                 sambungannya berada pada halaman lain.
9. Flowline menunjukan bagian arah instruksi yang dijalankan

RESISTOR

"arus yang mengalir melewati batang karbon sebanding dengan beda tegangan antara ujung-ujung batang karbon" (Ohm)

Hal ini pertama kali diketahui, dengan menggunakan sepotong kawat, oleh Gregor Ohm. sehingga fakta ini disebut sebagai Hukum Ohm. Hukum Ohm berlaku terhadap semua konduktor. kita dapat menuangnya kedalam persamaan :

Apabila tegangan listrik(V) dinyatakan dalam satuan Volt dan arus listrik(I) dalam satuan amp, maka satuan untuk tahanan listrik(R) adalah Ohm.

Didalam kebanyakan rangkaian lstrik kita menyambung-nyambungkan berbagai komponen rangkaian dengan menggunakan kawat-kawat tembaga. hal ini disebabkan karena tembaga adalah sebuah bahan konduktor listrik yang sangat baik. tembaga memiliki tahanan listrik yang sangat rendah.

akan tetapi, sejumlah sambungan pada rangkaian membutuhkan tahanan listrik yang lebih besar daripada apa yang dapat diberikan oleh kawat tembaga. inilah alasannya mengapa kita menggunakan Resistor. 

gambar diatas memperlihatkan sebuah Fixed resistor yang tipikal. kemudian lambang dari resistor itu sendiri dapat anda lihat pada gambar dibawah ini

 

STRIPBOARD

Papan stripboard merupakan sarana yang handal untuk membuat berbagai rangkaian elektronika. Stripboard sangat berguna apabila anda hendak membuat sebuah rangkaian hanya sekali saja.
Komponen-komponen rangkaian dipasang pada sisi permukaan stripboard yang kosong. Kaki-kaki dan kawat-kawat terminal komponen ditancapkan kelubang-lubang pada papan hingga tembus ke permukaan belakangnya. Kawat-kawat terminal dan kaki-kaki komponen disolderkan ke lempeng-lempeng (strip) tembaga yang terdapat di permukaan belakang papan stripboard.

     Dengan cara ini, kita dapat membuat sebuah rangkaian dengan memanfaatkan strip-strip tembaga  dibagian belakang papan sebagai jalur-jalur konduktor yang menghubungkan berbagai komponen rangkaian. kita dapat juga menggunakan kaawat-kawat tipis untuk menyambungkan suatu strip tembaga dengan strip lainnya.
     oh ya.... terkadang sebuah strip tembaga dipotong secara melintang untuk memisahkannya menjadi dua bagian atau lebih.
     Stripboard memiliki satu keunggulan, yaitu bahwa kita dengan mudah dapat mengadakan berbagai penyesuaian  pada rangkaian, setelah rangkaian selesai dibuat. hal ini membuat stripboard lebih menguntungkan untuk digunakan dalam membangun rangkaian-rangkaian prototipe. Rangkaian prototipe adalah versi paling awal dari suatu rangkaian tertentu, yang telah selesai dirancang namun belum teruji kinerjanya. Setelah pengujian dilakukan rangkaian - rangkaian ini mungkin harus mangalami modifaikasi untuk memperbaiki kinerjanya. sebagai contohnya, kita mungkin akan memutuskan untuk mengubah nilai-nilai beberapa komponennya , atau memperbaiki logika rangkaian. hal ini hampir mustahil dilakukan apabila rangkaian yang bersangkutan dibuat pada papan PCB.